1. Jika vektor a = (1 2 3), b = (5 4 –1), c = (4 –1 1) maka vektor a + 2b – 3c adalah.....
Jawab
a + 2b – 3c

2. Diketahui [a] = √3 , [b] = 1 dan [a-b] = 1 maka panjang vektor a + b adalah........
Jawab
3. Diketahui dua vektor a=2i-3j+4k dan b=5j+5k.nilai a.b adalah....
Jawab
a = 2i - 3j + 4k,
b = 5j + 5k = 0i + 5j + 5k
ab = 2(0) + (-3)(5) + 4(5) = 0 - 15 + 20 = 5
4. Diketahui la+bl=2√19, jika lal=4 dan lbl=6 maka la-bl adalah...
Jawab
|a +
b| = 2√19
|a + b|^2 = (2√19)^2
|a|^2 + 2ab + |b|^2 = 4(19)
4^2 + 2ab + 6^2 = 76
16 + 2ab + 36 = 76
2ab = 24
|a - b|^2 = |a|^2 - 2ab + |b|^2
|a - b|^2 = 4^2 - 24 + 6^2
|a - b|^2 = 28
|a - b| = √28 = 2√7
5. Diketahui vektor a=2i-3J+k, b=pi+2j-k dan c=i-j+3k. jika b tegak lurus terhadap vektor c, vektor a-b-c adalah....
Jawab
b . c = 0
(p,2,-1) x (1,-1,3) = 0
(p,-2,-3) = 0
p-2-3= 0
p = 5
a-b-c =
(2,-3,1)-(5,2,-1)-(1,-1,3) = (-4,4,-1)
6. Jika sudut antara vektor a=i+akar 2j+pk dan vektor b=i-akar 2j+pk adalah60 derajat,maka p adalah....
Jawab
7. Diketahui titik A(3, 2, -1) , B(1,-2,1) dan C(7,p-1, -5) segaris untuk nilai p...
Jawab
merupakan vektor posisi dari titik koordinat dengan mengacu kepada titik O ( titik pusat koordinat).
karena segaris, maka
Dari persamaan di atas dapat dilihat
bahwa :
-2 = 4k atau 2= -4k
k = -2/4
k = -1/2
masukkan nilai k pada persamaan -4 = k
(p-3)
-4 = k (p-3)
-4 = -1/2 (p -3)
p - 3 = -4 (-2)
p -3 = 8
p = 8 + 3
p = 11
Jadi nilai adalah 1
8. Diketahui titik A(3,1,-4) B(3,-4,6) dan C(-1,5,4) titik p membagi vektor AB sehingga AP:PB=3:2 maka vektor yang di wakili oleh vektor PC adalah...
Jawab
AP : PB = 3 : 2, maka




p = (3, –2, 2)
Jadi vektor PC
= c – p


Ditanyakan :
(a - 2b) . 3c = .... ?
Jawab :
a . b = 0
(p, 2, -1) . (4, -3, 6) = 0
p(4) + 2(-3) + (-1)(6) = 0
4p - 6 - 6 = 0
4p = 12
p = 3
a - b
= (p, 2, -1) - (4, -3, 6)
= (3, 2, -1) – (4,-3, 6)
= (-1, 5, -7)
2c = 2(2, -1, 3) = (4, -2, 6)
(a - b) . 2c
= (-1, 5, -7) . (4, -2, 6)
= -1(4) + 5(-2) + (-7)(6)
= -4 - 10 - 42
= -56
1. 11. Diketahui A(1,2,3), B(3,3,1), dan
C(7,5,-3). jika A,B, dan C segaris (kolinear) maka AB : BC adalah....
Jawab :
= (3,3,1) - (1,2,3)
= (2,1,-2)
BC = c - b
= (7,5,-3) - (3,3,1)
= (4,2,-4)
AB : BC
(2,1,-2) : (4,2,-4)
(2,1,-2) : 2(2,1,-2)
1 : 2
Jadi, AB : BC = 1 : 2
1. 12. Jika vektor tak nol a dan b memenuhi
|a+b| = |a-b| maka vektor a dan b saling...
Jawab :
|a+b| = √|a|² + |b|² + 2 |a| |b| . cos x
|a-b| = √|a|² + |b|² - 2 |a| |b| . cos x
√|a|² + |b|² + 2 |a| |b| . cos x =
√|a|²+|b|² + 2 |a| |b| . cosx
AKAR NYA HILANG JADI
|a|² + |b|² + 2 |a| |b| . cosx = |a|²+|b|²
+ 2 |a| |b| . cosx
=> |a| |b| . cos x + 2 |a| |b| . cos
x = 0
=> 4 |a| |b| . cos x = 0
=> 0/4 |a|.|b|
=> 0
cos x = 0 = 90°
1.
13. Diketahui titik A (2,7,8) B (-1,1,-1 dan
c ( 0,3,2 ) jika vektor AB mewakili vektor u dan BC mewakili vektor v proyeksi
orthogaonal vektor u pada v adalah...
Jawab :
1. 14. Diketahui Vektor a= 2i - 3j + 6k b = i +
pj - k saling tegak lurus. Nilai p adalah...
Jawab :
Saling tegak lurus, maka
a . b = 0
(2,-3,6) . (1,p,-1) = 0
2 + (-3p) + (-6) = 0
-3p - 4 = 0
p = -4/3
1. 15. iketahui vektor a=5i +j +7k dan b=3i-j
+2k. Proyeksi ortogonal vektor a pada b adalah...
Jawab :
16. Diketahui vektor a = 3,-2,1 dan b= 2,y,2. jika z proyeksi a terhadap b dan vektor |z|= 1/2|b|, maka nilai y yang memenuhi adalah....
Jawab :
|z| = ½ |b|
|z| = ½ √(2)² + (y)² + (2)²
|z| = ½ √y² + 8
a.b = (3, -2, 1) × (2, y, 2) = (6 - 2y + 2) = 8 - 2y
Proyeksi a pada b
|z| = a.b / |b|
½ √y² + 8 = (8 - 2y) /√y² + 8
½ (√y² + 8) (√y² + 8) = 8 - 2y
y² + 8 = 2 (8 - 2y)
y² + 8 = 16 - 4y
y² + 4y - 8 = 0
y=−2+2√3
atau −2−2√3
Jawab :

Pembuat nol
pertidaksamaan di atas adalah:
x =
−1 dan x = 2
Karena tanda pertidaksamaannya “≤” maka hasil
dari pertidaksamaan tersebut berada di antara pembuat nol.
−1 ≤ x ≤ 2
Jadi, nilai x yang memenuhi
adalah −1 ≤ x ≤ 2
19. Vektor u=2i-j+2k dan vektor v=4i+2j+4k adalah vektor searah?sebab nilai vektor u. v =18
pembahasan :
20.
 Reviewed by Shuun
on
Maret 03, 2021
Rating:
Reviewed by Shuun
on
Maret 03, 2021
Rating:




















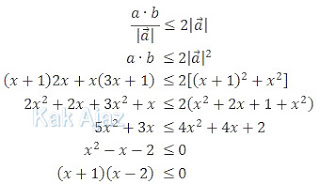




Tidak ada komentar: